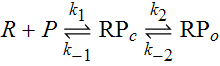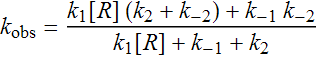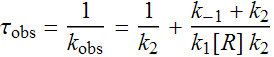In a previous post, we explored some of the properties of promoter sequences and some of the protein domains of RNP holoenzyme. The end product of a search of a DNA sequence for a promoter is the formation of a closed complex. This complex is the first on the path to productive transcription initiation. There are several intermediates in this whole process, and one or more of these reactions is regulated in almost all promoters, though the mechanistic details may differ. To apply knowledge of these steps in understanding regulation of any promoter in particular, we must examine the reaction kinetics of the formation of each of these intermediates. It is also valuable to play around with the parameters to get a feel for the overall process.
The discrete steps were defined and explored through experiment by Will McClure (PNAS, 77, 5634-5638, 1980). Here I will summarise his theoretical approach and a few of his experimental results.
Theory
McClure defines two steps prior to initation of transcription. First RNP bind to the promoter forming the closed complex. This is followed by an isomerization step during which RNP unwinds the DNA surrounding the +1 initiation site, providing access to the template for binding of the initial NTP (the +1 base in the RNA transcript). Along with this unwinding, the template strand must move into the active site of RNP. The process can be described by the simple rate equations,
with R, P, RPc and RPo representing free RNP, a promoter sequence DNA, the closed complex and open complex, repsectively. For the purposes of this experiment, [R]>>[P], a condition that may not hold in vivo. Nevertheless, this condition greatly simplifies the analysis in that we can assume a steady state for RPc. The rate equation that we are concerned with here is
Assuming that the equilibrium of the first reaction lies far to the right (k1>>k-1) , and that the kinetics of the reaction is fast, the steady state assumption can be applied for [RPc], d[RPc]/dt ≈0, and [RPc] ≈ Pt, the total amount of promoter in the reaction. We can derive a linear first order ODE
where α and β are comprised of the rate constants and the concentrations of P and R in the reaction. The solution of this should be familiar to those who have taken differential equations
when k-2 ≈ 0, then β/α = [Pt] and α = kobs
with α being kobs yielding,
Equation (1)
where
This can be simplified by the assumption, k-2 << k2, to
The reciprocalof kobs, τobs, is the average time it takes to form RPo.
To understand what is going on, let’s look at how [RPo] changes over time with three different [R] concentrations. For convenience, I chose Pt = 1. As one would expect from the theoretical considerations embodied in Eq. (1), over time [RP0] increases and approaches Pt.
Although we could get a measure of τobs from this type plot, one could imagine making accurate measurements as each concentration increases might prove difficult to accurately measure exactly when [RPo] = 0.63 (the concentration at t = τobs).
The experimental questions are: how can we measure RPo and is there a better way to plot the data? Previous work led to the finding that if you leave out one or more NTP in a transcription reaction, RNP will catalyze the synthesis of short transcripts only a few nucleotides long that rapidly fall out of the open complex, with RNP immediately reinitiating transcription. Under these conditions, the open complex spews out these short transcripts at a constant rate. These are called abortive initiation products and can be measured. Thus we can determine the concentration of RPo by assaying the rate of abortive initiation. As a side note, abortive initiation occurs in vitro at most promoters even in the presence of all NTP.
Given that we can measure RPo, how can we measure τobs? Since the rate of abortive inititation is proportional to RPo, we can measure the rate of abortive product formation and this will reflect [RPo]. If we incubate RNP and promoter for a sufficient time to completely drive all of the initiation complexes into RPo and then add NTP at t = 0, plotting abortive transcript concentration versus time, we expect a straight line of data points with the line passing through the origin. The slope of the line is a function of the concetration of Pt and the synthesis rate of abortive products characteristic of that promoter. In a separate reaction, RNP, promoter, and NTP are mixed at t = 0. Because of the time required to form RPo, there is a lag before the slope of the data points becomes the same as (i.e. parallel to) the preincubated reaction. Extrapolating a line through the measurements of the concentration of abortive products and determining where it intersect gives a measure of τobs. If we vary [R] we expect a shift of this intersection but should not affect the slope of the line. The following is a theoretical plot the amount of abortive transcripts produced using the same concentrations of [R] shown above multiplying [RPo] by a constant (the rate constant for abortive initiation). The thin black lines here are the extrapolation of the slope of each curve once a constant slope is achieved.
 As you can see, we can take many more data points over a longer period of time to get an accurate measure of the slope and the intercept, τobs. How does this compare to real life? Figure 1 from the manuscript shows some experimental results.
As you can see, we can take many more data points over a longer period of time to get an accurate measure of the slope and the intercept, τobs. How does this compare to real life? Figure 1 from the manuscript shows some experimental results.
Now taking τobs and plotting versus 1/[R] we obtain a line with the vertical intercept being 1/k2. McClure shows some data for two different promoters:
If this figure reminds you of Michaelis-Menton kinetics, you would be correct, and many of the underlying assumptions and analyses are the same, but here we are not measuring the final product of a biochemical reaction. Instead, we are capturing RNAP in the act, giving us a glimpse into its modus operandi.
Further information can be obtained from the slope of the lines. These critically depend upon the numerator in the τobs equation,: k-1 + k2. With the basic assumption that k-1>>k2, the numerator reduces to k-1 and the slope becomes k-1/k1k2, which McClure defines as kon. Since k1 is the bimolecular rate constant that arises from the collision of the promoter and RNAP, it should be the same regardless of the promoter. Therefore, the slope reflects the ratio of k-1/k2 for a given [R]. Those promoters with a lower k-1, i.e. tighter binders, will have a shallower slope compared to those that have a higher k-1. The importance of kon can easily seen at lower RNP concentrations: as [R] becomes lower (i.e. 1/[R] increases), the difference between rates of initiation at promoters with different kon increases.
This work became a firm theoretical framework for many mechanistic studies that followed, and as we move toward modeling transcription in vivo, we need to keep these concepts in mind. McClure also points out something that I think is under appreciated: the transition from closed to open complex is rather slow, with the transition taking a few seconds to several minutes (or even longer). This dynamic range can be tuned by direct interaction with transcription factors or influenced by cellular conditions, for example DNA supercoiling or free RNA polymerase concentration. The interplay between all of these influences presents a challenge to researchers trying to either understand how cells work or for engineers trying to design cells to make useful products.